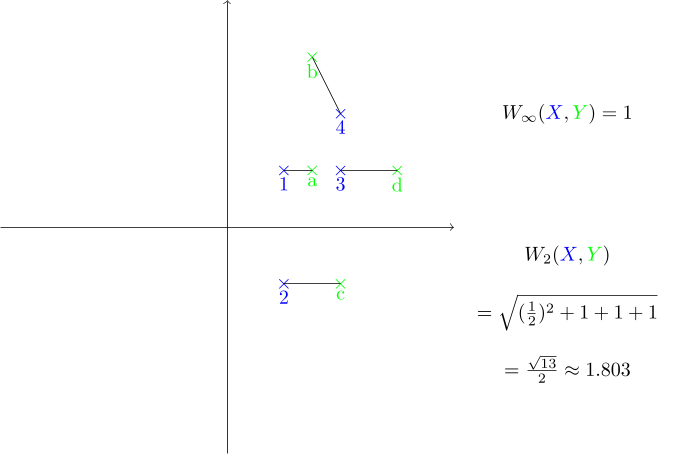0.1 Contact info¶
| My name: | Julian Brüggemann |
| My office: | IMPAN |
| ul. Sniadeckich 8, 00-656 Warszawa | |
| Office: 17 | |
| My office hours: | Wed & Thu: 10-12 |
| My email address: | julian.brueggemann@impan.pl |
| Lecture: | Tuesdays: 16:15-18:00 |
| Location: | MIM UW, Room 4050 |
| Exercise classes: | John Rick Manzanares |
| Time: | Tuesdays: 18:15-20:00 |
| Location: | MIM UW, Room 4050 |
| His office: | IMPAN |
| ul. Sniadeckich 8, 00-656 Warszawa | |
| Office: 16 | |
| His office hours: | Tue & Thu: 9-11 |
| His email address: | jdolormanzanares@impan.pl |
0.2 Course dates, homework, and exams:¶
Lecture period: 25.02.-10.06.2025 No lecture and exercise on 22 of April! (spring vacation)
How to pass the class:
Semester Project (50%): Either theoretical or applied.
For Master Students:
Theoretical: Write an expository text with definitions, examples etc. on some theoretical topic of the lecture.
Applied: Write an expository tutorial (including code) on some software (including applying it to some data set)
For PhD students:
Same, but not only on contents of the lecture direcly but also on a research paper related to lecture contents.
Homework: 2 excercises per week, can add bonus points to the Semester project grade (need to present at least one homework exercise in class).
Oral exam (50%)
You will have to answer questions and explain concepts from the lecture. You can choose the beginning of the exam by starting with your favourite Algorithm/Concept/Theorem/Application (from the lecture).
Official exam periods:
23.06.-06.07. (preferred: 30.06.-04.07.)
01.09.-14.09. (preferred: 09.09.-14.09.)
Both need a passing grade to pass the course!
1. What is topological data analysis?¶

What is data?¶
Anything can be data, if it is interesting enough!
Often measurments of some kind:
-physics: energy, momentum, location
-social sciences: Number of people of a certain group, answes to a poll, opinions, votes in elections
-often: data points are collections of numbers (or interpreted in that way: e.g. vectorization)
-special case: time dependent data - time series
Want to find: patterns, meaning, general rules
1.1 What is TDA?¶
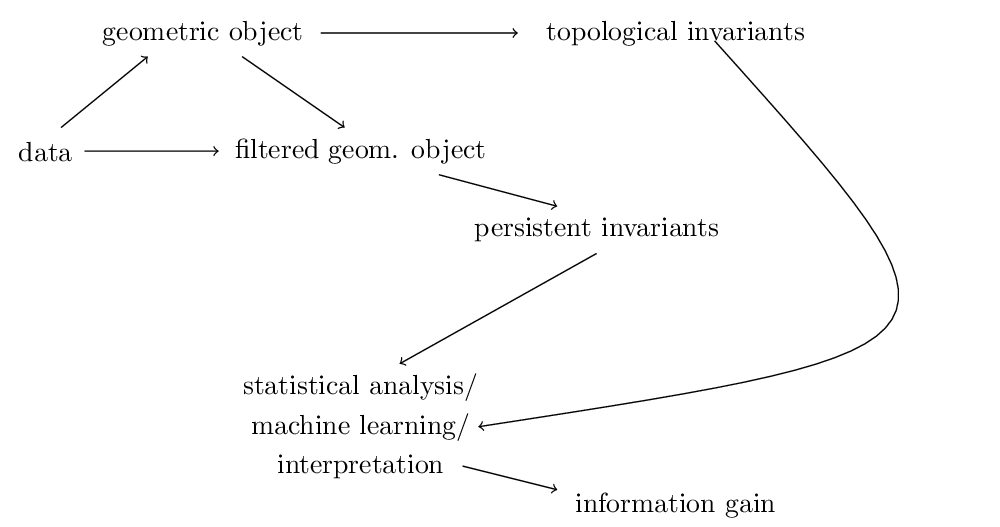
1.1 What is TDA?¶
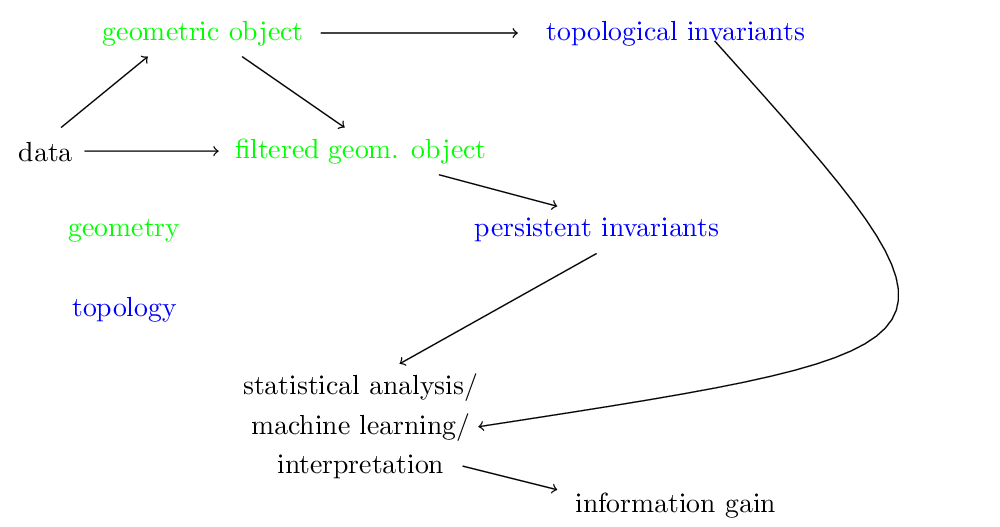
1.2 An overview of topology¶

In data:
-Is an image zoomed in/out or distorted?
-Is it the same data set just with different coordinates?
-Topological features might indicate interesting phenomena.
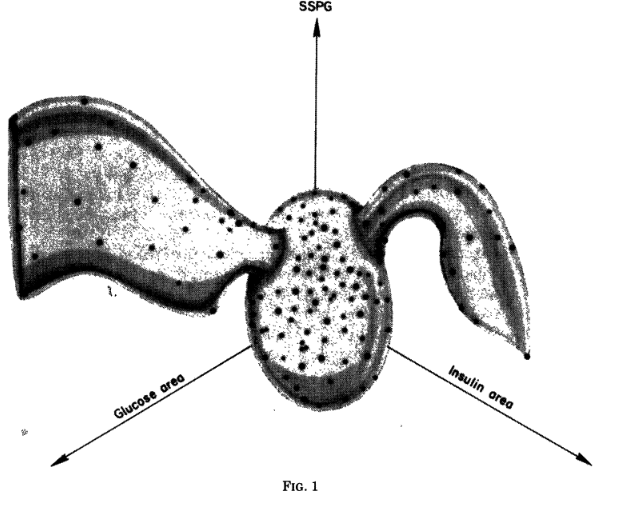
Types of geometric objects¶
| (Smooth/differentiable) Manifolds | (simplicial/cubical/CW) Complexes | topological/metric spaces |
|---|---|---|
| -locally given by parametrizations/solutions to differentiable equations | -result of successive gluing instructions | -given by a set of points +topology/metric |
| -locally Euclidean $\cong \mathbb{R}^n$ | -built out of simple building blocks: simplices/cubes/cells | -local neighborhoods might be complicated |
| -have chart transfer maps/an atlas | -have skeletal filtration | -no canonical decomposition |
| -may be embedded in $\mathbb{R}^n$ or abstract | -may be geometrically embedded or abstract | -no canonical embedding |
| -notion of dimension coming from $\mathbb{R}^n$ | -notion of dimension coming from building blocks $\Delta^n, I^n, D^n$ | -no general notion of dimension |
| -tools from differential topology/geometry | -tools from combinatorial topology/geometry | -tools from point set topology |
| -to computers only directly accessible via parametrizations/systems of differentiable equations | -to computers accessible via various graph structures (simplex tree/face poset/cliques in the 1-skeleton/...) | -in this generality, only finite spaces are directly accessible to computers |
Examples:¶
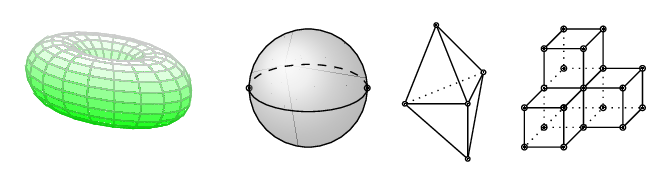
For manifolds and complexes:
-have a standard way of visualization if dimension is low enough, given by an embedding in Euclidean space.
-have two notions of distance: intrinsic and extrinsic.
The manifold hypothesis¶
In many fields of science: phenomenea described by differential equations
$\Rightarrow$ solutions lie on manifolds subject to these equations
Manifold hypothesis: Data points are sampled around manifolds. Often, the dimension of the manifold is much lower than that of the ambient space.
The curse of dimensionality¶
Combinatorial explosion:
| manifolds | complexes |
|---|---|
| sampling problem: | combinatorial explosion |
| exponential growth in volume $\Rightarrow$ exponential growth in number of needed points | $\Delta^n $ has $2^{n+1}-1$ simplices $\rightarrow$ exponential growth |

The curse of dimensionality¶
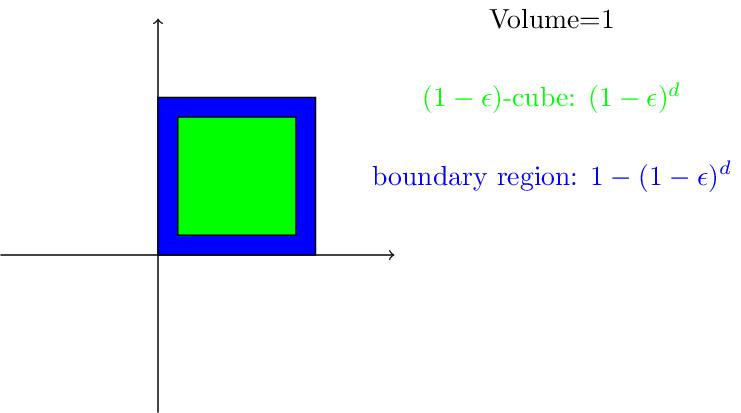
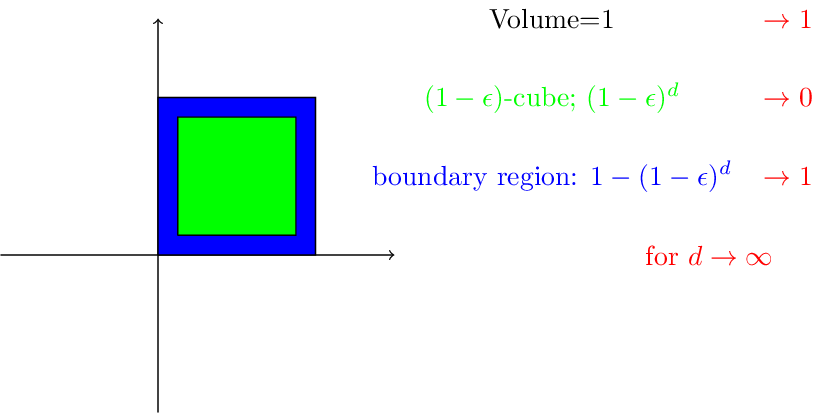
Concentration of measure:
-Volume is concentrated in the boundary. Small changes in radius lead to high changes in number of needed sample points
-Measurement error gets more significant than structure of manifold
$\Rightarrow$ Need dimension reduction before finding the manifold without changing the topological properties
Alternative: Notion of volume is induced from notion of distance - use a different notion of distance optimized for the dataset to counteract the curse of dimensionality
Metric and topological spaces¶
Space: Set of points $X$ together with extra structure
Metric space: extra structure is a metric $$ d\colon X \times X \rightarrow \mathbb{R}_{\geq 0}\\ d(x,y)=d(y,x) \\ d(x,y) + d(y,z) \geq d(x,z)\\ d(x,y)=0 \Rightarrow x=y $$
Abstract spaces:
advantages: do not have to deal with parametrizations/gluing maps
disadvantages: have no idea what they look like
Remedy: $\epsilon$-balls: $B_\epsilon(a) := \{x \in X \rvert d(x,a)<\epsilon\}$
Examples:¶
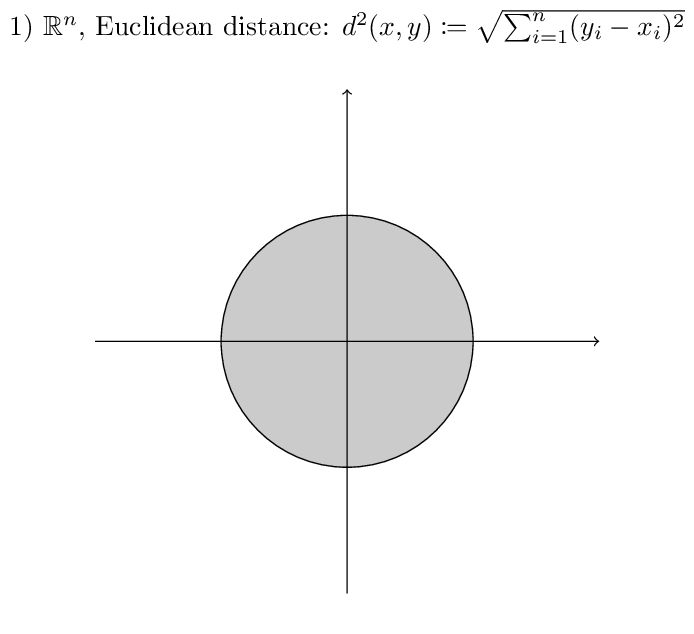
Examples:¶
Examples:¶
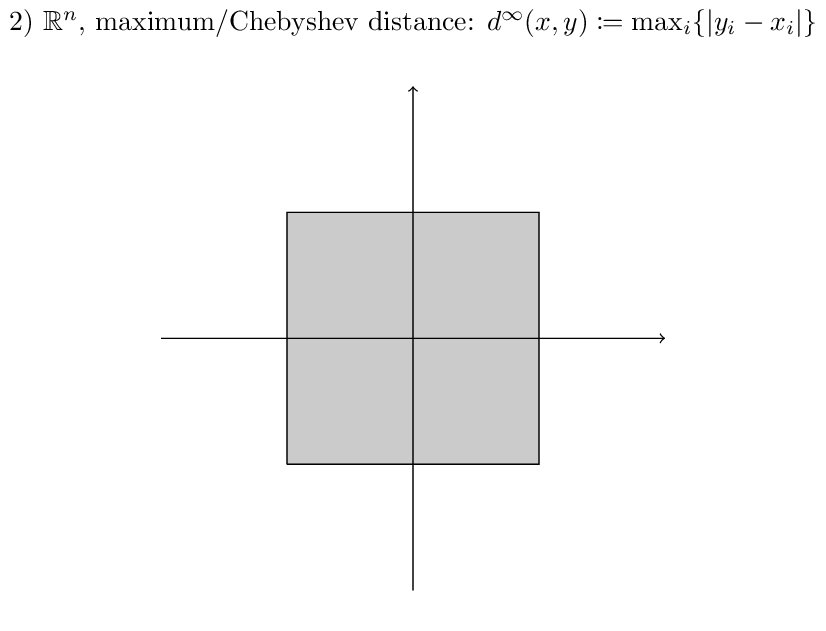
Examples:¶
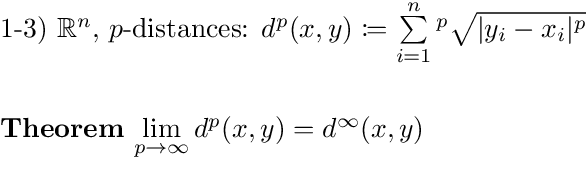
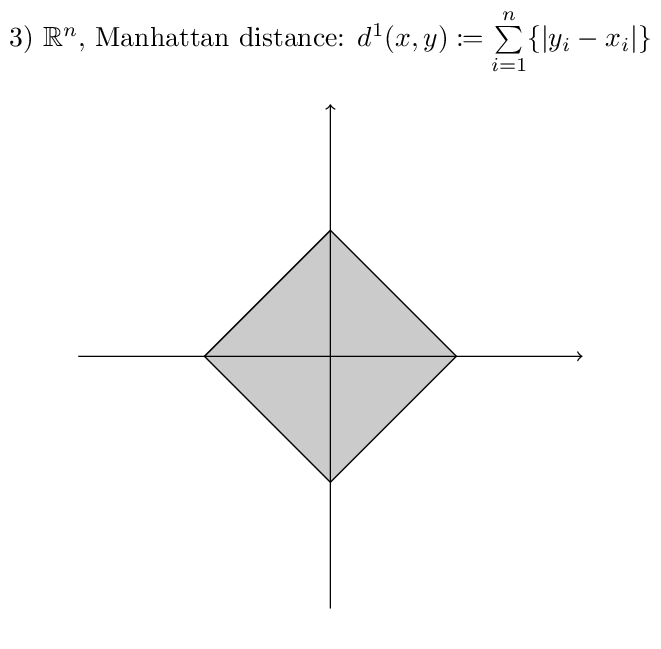
Examples:¶

Examples:¶
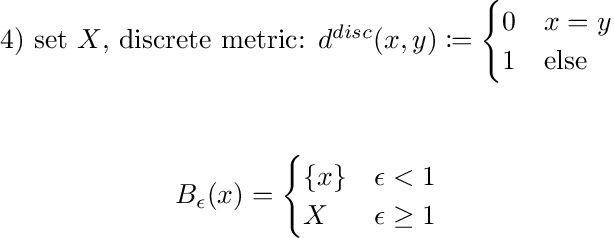
Examples:¶
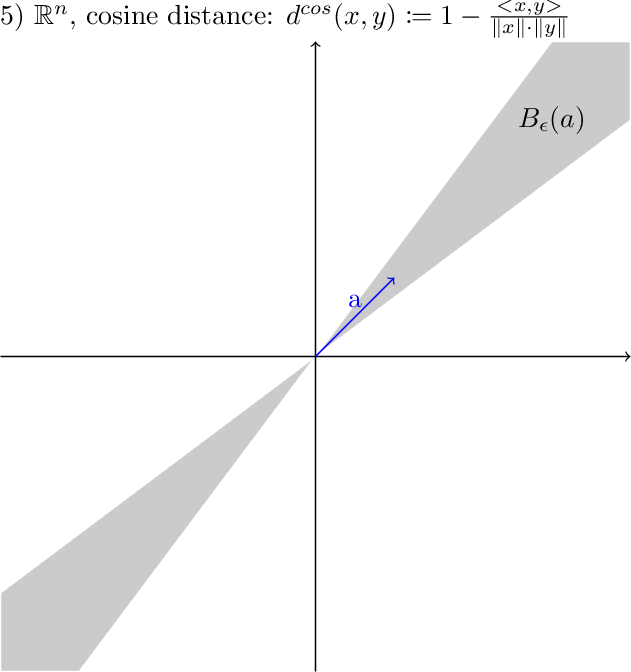
Is this a metric?
Why not?
Topological spaces¶
Definition: Let $X$ be a set. A topology on $X$ is a collection $\tau$ of subsets $U\subseteq X$ such that
- $\emptyset,X\in \tau$
- $U_1,\dots,U_n \in \tau \Rightarrow \bigcap\limits_{i=1,\dots,n}U_i \in \tau$
- $\{U_i\}_{i\in I} \in \tau \Rightarrow \bigcup\limits_{i \in I} U_i \in \tau$
The $U_i$ are called open sets.
Metrics versus Topology¶
Metric spaces are topological spaces:
The $\epsilon$-balls generate a topology via arbitrary unions.
How do we understand topological spaces?
Via maps between them!
Definition
A map between topological spaces $f \colon (X,\tau_X) \rightarrow (Y,\tau_Y)$ is called continuous if for all $U\in \tau_Y, \ f^{-1}(U) \in \tau_X$.
A map is called a homeomorphism if it is continuous, bijective, and its inverse is continuous.
Criteria for continuity¶
If $f$ is a map between metric spaces, then continuity is equivalent to $\epsilon-\delta$ continuity and sequence-continuity.
If $f$ is differentiable, then $f$ is continuous.
Examples:¶

Examples:¶

Examples:¶

For topological purposes:¶
Definition:
A metric is called finite is $\sup\limits_{x,y\in X} d(x,y) < \infty$.
Two metric are called equivalent if they induce the same topology.
Proposition:
Every metric $d(x,y)$ is equivalent to a finite one.
Idea of proof.
Check that
$$d'(x,y) := \frac{d(x,y)}{1+d(x,y)}$$is bounded by 1 and equivalent to $d(x,y)$.
Lipschitz maps¶
Definition:
A map between $f: X \rightarrow Y$ metric spaces is called Lipschitz continous with respect to a parameter $L$ if $$d_Y(f(x),f(y))\leq L \cdot d_X(x,y). $$
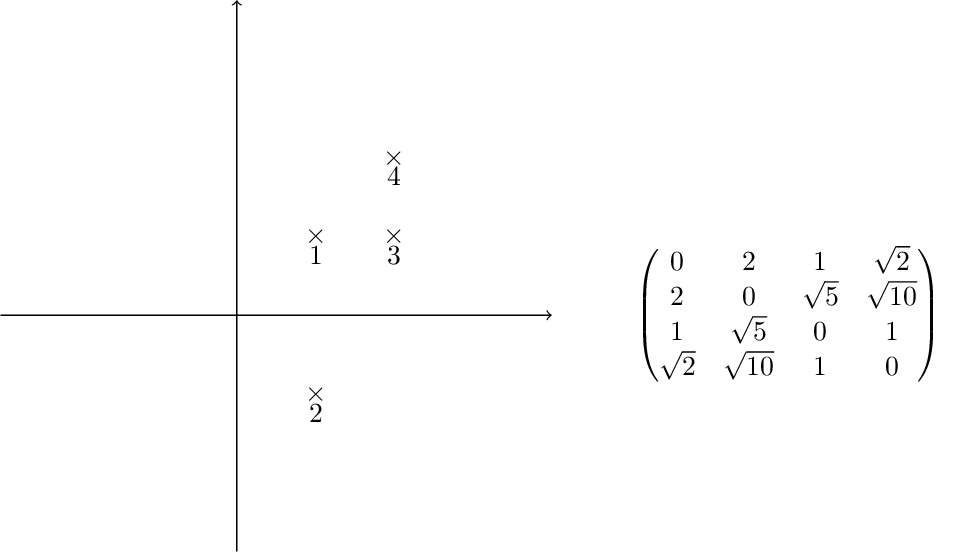
Point clouds as finite metric spaces¶
For a finite set $X\subset \mathbb{R}^n$, we can restrict the ambient metric to $X$
$\rightarrow$ turn $X$ into a finite metric space.
We can store the distances more conveniently in the distance matrix:
Distances for point clouds¶
Given two point clouds, what is their distance from each other?
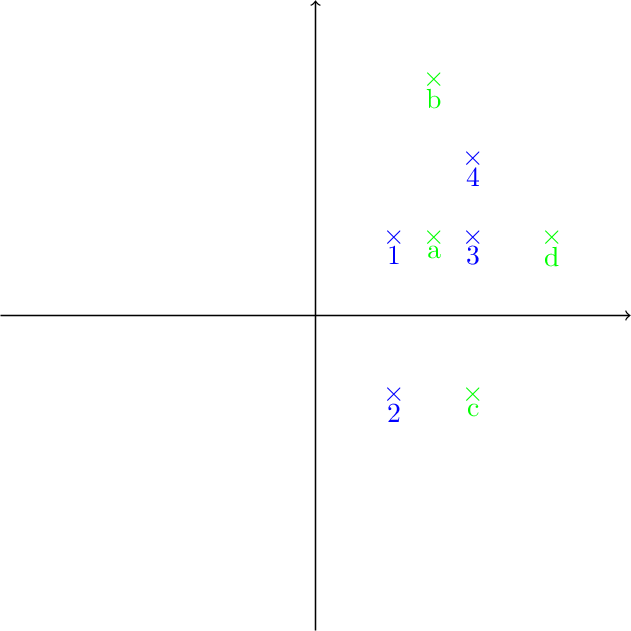
The Bottleneck and Wasserstein distances¶
Definition
Let $X,Y$ be finite point clouds such that $\lvert X \rvert = \lvert Y\rvert$. The Bottleneck distance $W_\infty$ is defined by
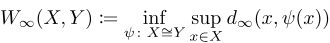
The Wasserstein q-distance $W_q$ is defined by
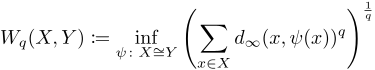
In our example:¶